[Graphics] Projection, Reverse-Z Projection
다음 내용들을 다룹니다.
- Projection 과정
- Reverse-Z Projection 개념
1. Projection
벡터를 다른 벡터나 공간으로 투영하는 것입니다.
게임에서 일반적으로 사용되는 Projection
perspective projection : 3D 공간상의 게임을 2D 모니터에 보여주기 위해 사용합니다. 멀리 있는 물체가 가까이 있는 물체보다 작게 보이는 원근법이 적용됩니다.
3 차원 공간상의 임의의 점 ${v}$ 가 Perspective Camera 를 통해 화면에 Projection 되는 과정
우선, view transform을 통해 world space에서 camera space로 변환해 줘야 합니다.
EYE : 카메라 위치
AT : 카메라가 보고 있는 기준점
UP : 카메라의 위 벡터
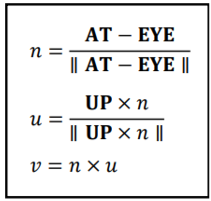
이렇게 {u,v,n, EYE}인 camera space를 {e1,e2,e3,O}인 world space로 변환하는 것이 view transform입니다. (행 우선으로 작성하겠습니다.)
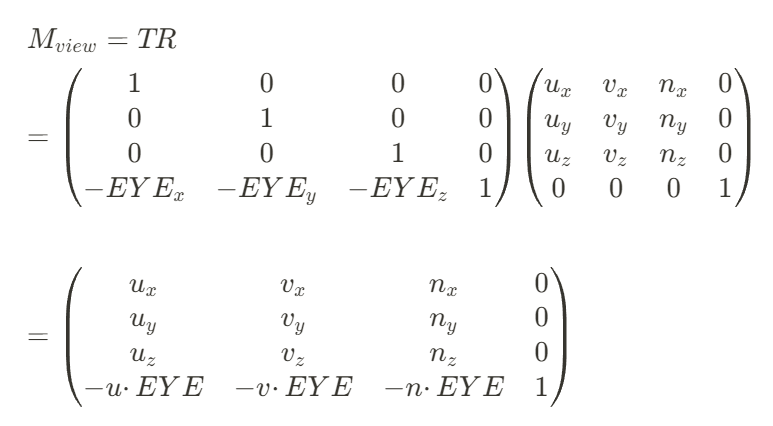
그 후, projection transform을 통해 camera space에서 clip space로 변환해 줘야 합니다.
camera는 시야(field of view)가 제한적이기 때문에 씬에 있는 모든 오브젝트를 볼 수 없습니다. 볼 수 있는 지역을 절두체(view frustum)라고 합니다. 절두체는 fovy(y축 시야각), aspect(w/h, 가로 세로 비율), n(near plane z축 거리), f(far plane z축 거리) 4개의 파라미터로 이루어진 truncated pyramid 모양입니다. projection transform을 통해 절두체 카메라 공간을 2*2*1 크기의 직육면체 클립 공간으로 투영합니다. (Clip space 범위를 Direct3D 기준으로 하겠습니다.)
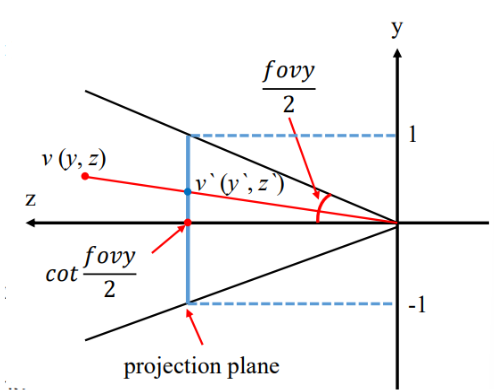
projection plane을 z = cot fovy/2 에 직교하게 두면
camera space에서의 점 v(x, y, z, 1)를 projection plane에 투영한 점 v’(x’, y’, z’, 1)는 삼각형의 닮음을 이용해서 구할 수 있습니다.
$x’ = cot\frac{fovx}{2}\frac{x}{z}$
$y’ = cot\frac{fovy}{2}\frac{y}{z}$
aspect도 구할 수 있습니다.
$aspect = \frac{W}{H} = \frac{tan\frac{fovx}{2}}{tan\frac{fovy}{2}} = \frac{cot\frac{fovy}{2}}{cot\frac{fovx}{2}}$
$cot\frac{fovx}{2} = \frac{cot\frac{fovy}{2}}{aspect}$
를 이용해서
$x’ = cot\frac{fovx}{2}\frac{x}{z} = \frac{cot\frac{fovy}{2}}{aspect}\frac{x}{z}$
x’를 이렇게 표현해 주면, v’는 aspect와 $cot\frac{fovy}{2}$로 표현할 수 있게 됩니다.
aspect를 A, $cot\frac{fovy}{2}$를 D라고 하면
$v’ = (x’, y’, z’, 1) = (\frac{D}{A}\frac{x}{z}, D\frac{y}{z}, z’, 1)$
동차 좌표계이기 때문에 w = z로 하면
$zv’ = (\frac{D}{A}x, Dy, zz’, z)$
점 v를 점 v’로 변환하는 projection transform은,
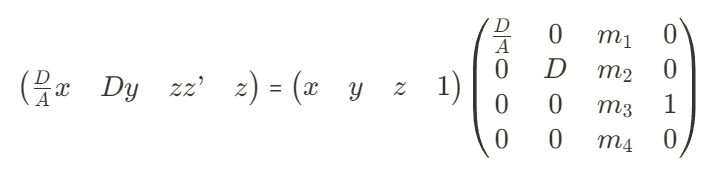
근데 z’는 점 v의 x좌표 y좌표와는 관련이 없기 때문에 이렇게 나타낼 수 있습니다.
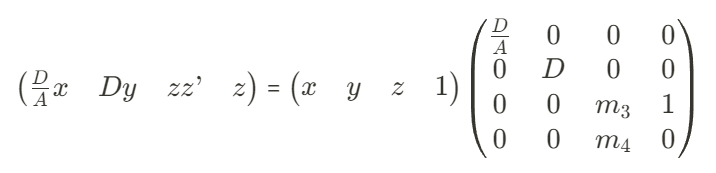
$zz’ = m_3z + m_4$ 이고
$z’ = m_3 + \frac{m_4}{z}$ 입니다.
Direct3D clip space의 z값 범위인 [0,1]에 따라
z가 n일 때는 z’를 0으로, z가 f일 때는 z’를 1으로 두면,
$1 = m_3 + \frac{m_4}{f}$
$0 = m_3 + \frac{m_4}{n}$
으로 표현할 수 있고, 연립방정식을 풀면
$m_3 = \frac{f}{f-n}$
$m_4 = \frac{-fn}{f-n}$
을 구할 수 있습니다.
따라서, projection transform은
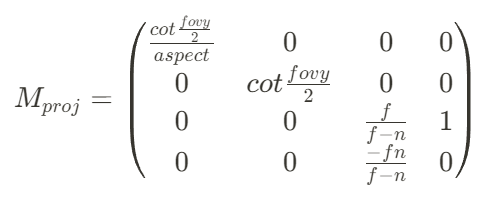
입니다.
projection transform까지 적용하면 동차 좌표계에서 w에 해당하는 부분이 z가 됩니다. 그래서 z로 나눠주는 perspective division을 해줍니다. 만약 점 v가 카메라로부터 z축 거리가 멀리 있었다면 더 크게 나눠지고, 가까이 있었다면 더 작게 나눠지면서 원근법이 적용이 됩니다. (NDC 공간)
이제 viewport transform을 통해 NDC 공간(2x2x1)에 있는 점을 카메라 화면 해상도에 맞게 Screen Space로 변환해 주면 됩니다.
원점(0,0)을 화면의 왼쪽 위 모서리로 두겠습니다.
Scaling :
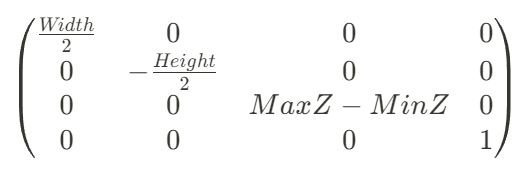
Translation :
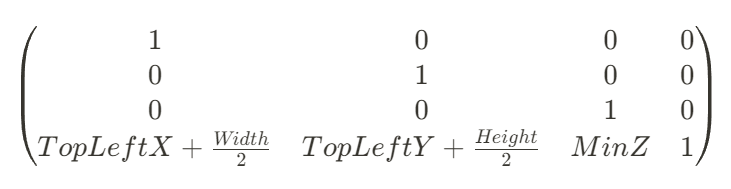
둘을 합치면,
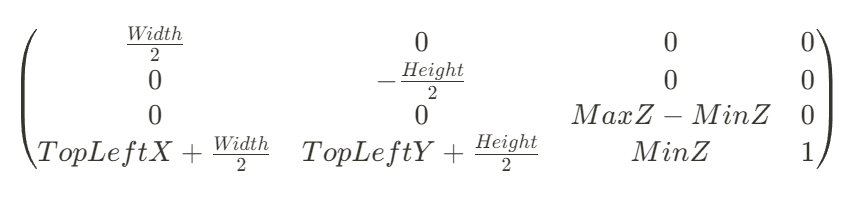
만약 카메라 화면 전체를 사용해 TopLeftX = 0, TopLeftY = 0. 그리고 MinZ = 0, MaxZ = 1이라고 하면
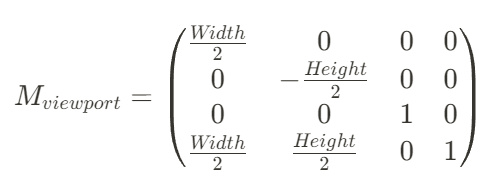
2. Reverse-Z Projection
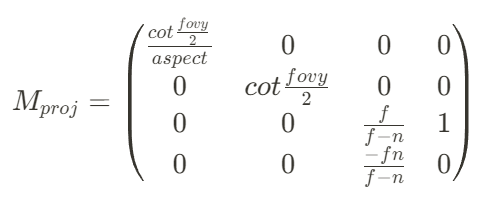
점 v (x, y, z, 1)에 projection transform을 적용하면 점 v’(zx’, zy’, zz’, z)가 되고
여기서 점 v’의 깊이값은,
$zz’ = \frac{f(z-n)}{f-n}$
에다가 동차 좌표계에서 w인 z를 나눠준
$z’ = \frac{f(z-n)}{z(f-n)}$
이 됩니다.
여기에 Near Plane Z축 좌표인 n이 0.1, Far Plane Z축 좌표인 f가 1000이라고 하면
$z’ = \frac{1000(z-0.1)}{z(999.9)}$
가 됩니다.
z가 0.1이라면 z’가 0.0이고,
z가 1이라면 z’가 0.9이고,
z가 10이라면 z’가 0.99이고,
z가 1000이라면 z’가 1.0 입니다.
즉, z가 Near Plane과 가까울 때의 깊이값의 변화가 크지만 Far Plane에 가까워지면 깊이값의 변화가 매우 작아집니다.
그래서 Far Plane 근처에 있는 원거리 객체들은 깊이값이 실제로는 동일하지 않지만, 깊이값의 차이가 매우 작은데 거기에 더해 부동소수점의 정밀도의 한계로 인해서 깊이값이 동일하게 처리될 수 있습니다. 이로 인해 Z-fighting 문제가 생길 수 있습니다.
Reverse-Z Projection은 Near Plane과 Far Plane의 깊이값을 서로 바꿔 원거리 객체들의 깊이값 정밀도를 올리는 방법입니다.
위의 projection transform을
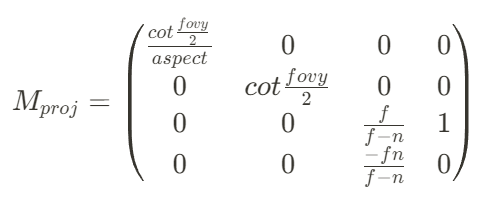
아래 것으로 바꾸는 것입니다.
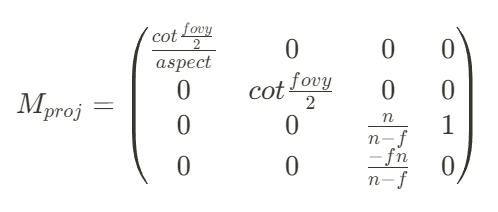
장점 :
오픈 월드 게임 등 Far Plane이 아주 멀리 있는 경우에는 View Frustum에서 가까이 있는 객체들보다 멀리 있는 객체들의 비중이 더 클 가능성이 큽니다.
Reverse-Z Projection을 하지 않으면
- 먼 거리에 있는 더 많은 객체들의 깊이값 변화가 작게 표현되게 되고,
- 부동소수점은 값이 클수록 정밀도가 떨어지는데 먼 거리 객체들이라 [0,1] 범위에서 1에 가까운 더 큰 값을 가지게 됩니다.
If we do the math, we can see that out of the total range between 0.0 and 1.0, only approximately 0.79% of all representable values are between 0.5 and 1.0, with a staggering 99.21% between 0.0 and 0.5. I always knew there was more precision near 0, but I don’t think I’d fully appreciated by quite how much.
출처 : https://tomhultonharrop.com/mathematics/graphics/2023/08/06/reverse-z.html
이로 인해 Z-Fighting 문제가 더 많이 발생할 가능성이 큽니다.
Reverse-Z Projection을 사용하면 멀리 있는 더 많은 객체를 깊이값의 변화를 크게 줄 수 있고, 더 작은 값을 가지게 해서 부동소수점 정밀도를 높여 이 문제를 해결할 수 있습니다.
Leave a comment