Inverse Kinematics
다음 내용들을 다룹니다.
- IK와 FK의 차이
- IK Solver 종류
- Numerical한 방법
- Heuristic한 방법
- 게임에서의 IK
- Two-Bone IK
Inverse Kinematics
순운동학(Foward Kinematics)과 역운동학(Inverse Kinematics)
FK는 회전 각도를 사용해 끝점의 위치를 계산하는 기술입니다. 관절의 회전 각도를 수동으로 적용해서 관절과 끝점을 원하는 위치에 둘 수 있습니다.
IK는 원하는 끝점 위치에 대해 자동으로 관절의 회전 각도를 구하는 방법입니다.
따라서 FK는 미리 회전 각도를 계산해둬야 하는 대신 원하는 자세(관절과 끝점)를 정확하고 빠르게 만들 수 있고, IK는 미리 계산해둘 정보는 없지만 원하는 끝점 위치가 주어졌을 때 제한 조건(관절이 회전 가능한 각도 등)을 고려해서 관절의 회전 각도를 계산하는 과정이 필요합니다.
IK Solver 종류
Numerical한 방법과 Heuristic한 방법으로 나눌 수 있습니다.
Numerical한 방법
데카르트 공간에서의 비선형 방정식 집합의 local minimum을 찾는 방법입니다. 이 local minimum을 찾는 여러 방법들이 있습니다.
- Jacobian based methods
Jacobian은 편미분을 통해 비선형 변환의 선형 근사치를 구하는 방법입니다. 캐릭터 관절의 회전 각도로 끝점의 위치를 구하는 함수는 각 관절이 다른 관절의 영향을 받기 때문에 비선형 방정식의 집합입니다. 그 함수의 Jacobian을 사용하면 관절의 회전 각도를 넣어서 끝점 위치 변화량의 근사치를 얻을 수 있는 것이죠. 이것이 FK식 접근입니다.
$\vec{𝑒} =J∆θ$
여기서 Jacobian을 왼쪽으로 넘겨준다면,
$J^{-1}\vec{𝑒} =∆θ$
즉, Jacobian의 역행렬을 통해 끝점의 위치 변화를 가지고 관절의 회전 각도를 구할 수 있습니다. 이를 통해 IK를 구현할 수 있습니다. 캐릭터 관절의 회전 각도로 끝점의 위치를 구하는 함수를 그대로 쓰지 않고 Jacobian을 적용하는 이유는 이처럼 IK를 구현하려면 역행렬이 필요한데, 비선형의 경우는 역행렬을 구하기가 어렵기 때문입니다.
그러나 Jacobian이 역행렬이 없거나, bone이 짧아 끝점이 닿을 수 없는 경우처럼 해가 없는 경우(singularity problem)에는 이것이 적용이 안 됩니다. 그래서 Jacobian의 local minimum을 구하는 Jacobian Pseudo-inverse을 사용합니다. 이를 얻는 접근법도 다양합니다. (Moore-Penrose pseudo-inverse, Pseudo-inverse Damped Least Squares 등)
- Newton Methods
$F(θ) = s_d – f(θ) = 0$
s_d는 원하는 끝점 위치입니다. f(θ)는 캐릭터 관절의 회전 각도로 끝점의 위치를 구하는 함수입니다. θ 값을 여러 번 넣어서 원하는 끝점 위치와 f(θ)의 값의 차이가 최소화되는 θ를 구하는 방법입니다.
테일러 급수를 사용해서 F(θ)를 근사합니다.
테일러 급수는 아래와 같습니다.
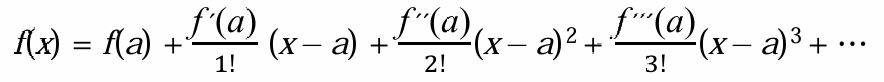
우측항을 끝까지 무한대로 만드는 것이 아니라 적절히 만들어서 근사 함수를 구합니다. 어떤 한 지점 a에 대해 근사 함수를 만들면, 그 주변의 일정 구간에서도 값이 근사하게 나옵니다.
따라서 처음 각도(θ_0)에 대해 근사 함수를 만들고 회전 각도(θ_0 + dθ)를 대입해서 s_d – f(θ)을 최소화 하는 dθ를 구하는 것이죠.
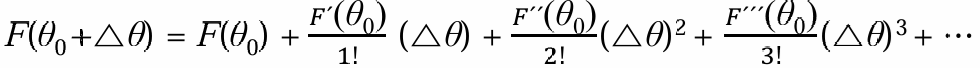
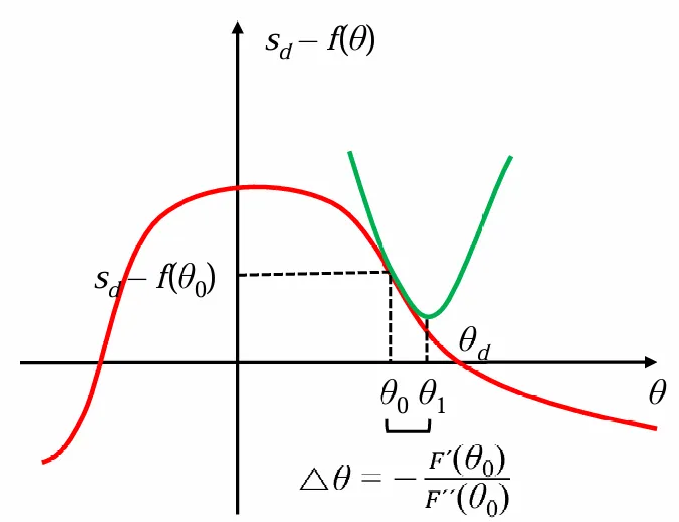
처음 각도에 대해서 적당히 2차 테일러 급수를 구하고, 그 테일러 급수의 기울기가 0인 곳을 검사하는 것을 반복하는 방법으로 값을 최적화합니다. 위 그림은 단일 변수 함수이지만, IK는 다변수 함수라 saddle point가 있기에 Hessian(이차미분)이 사용됩니다. Hessian 계산이 복잡하기 때문에 성능을 올리기 위해 Hessian의 근사치를 사용하는 Quasi-Newton Methods도 있습니다.
Heuristic한 방법
Numerical한 방법들은 계산이 복잡하고 느리기 때문에 대충 잘 동작하는 Heuristic한 방법들을 사용하기도 합니다. 게임에서는 특히 그렇죠.
- Cyclic Coordinate Descent
체인의 끝점 바로 전 관절에서 체인의 시작 관절 방향으로 관절들을 순차적으로 돌면서, 그 관절과 끝점을 잇는 선과 그 관절과 목표 끝점 지점을 잇는 선 사이 각도만큼 관절을 회전합니다. 그리고 원하는 결과를 얻을 때까지 이 전체 과정을 반복합니다.
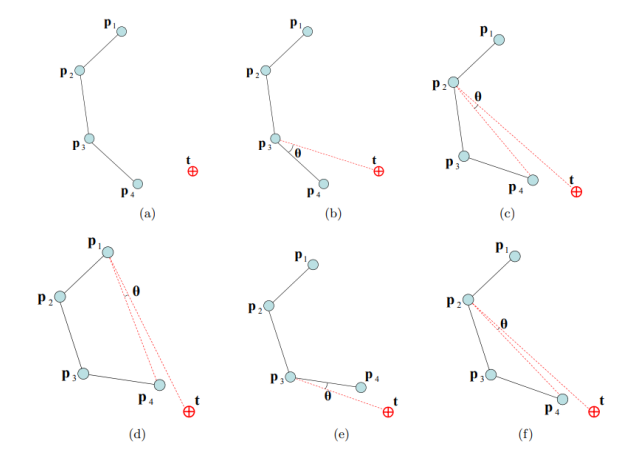
(a)가 처음 모습이고, (b)는 p3 관절과 p4사이 직선과, p3관절과 목표 끝점 위치 t 사이 직선 사이 각도인 θ만큼 회전하는 것입니다.
- Triangulation IK (Two-Bone IK에 사용)
제2코사인법칙은 삼각형에서 두 변의 길이와 그 사이각을 알 때 나머지 한 변의 길이를 구하는 방법입니다.
$c^2=a^2+b^2−2ab⋅cos(C)$
제2코사인법칙을 사용해서 체인의 시작 관절부터 시작해서 끝점 바로 전 관절 방향으로 관절들을 오직 한 차례 돌면서, 현재 관절에서 시작하는 bone의 길이 a와 나머지 bone들의 길이의 합 b와 현재 관절에서 원하는 끝점 위치까지의 길이 c를 이용해서 현재 관절에서 시작하는 bone을 제외한 나머지 bone들의 끝이 원하는 끝점에 닿을 수 있게 하는 현재 관절의 회전 각도를 구하는 방법입니다.
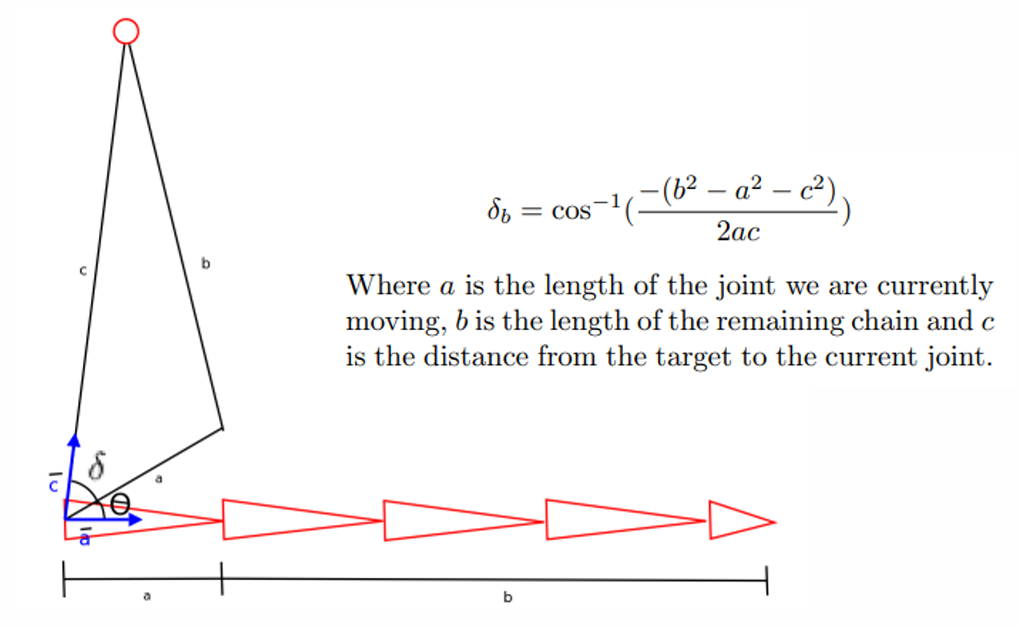
이 방법은 오로지 관절들을 한 바퀴만 돌면 되기 때문에 CCD보다 빠릅니다. 근데 이 방법은 원하는 위치가 있는 관절이 오직 끝점 한 개인 문제에만 적용할 수 있습니다. 왜냐하면 체인의 시작 관절에 대해 계산하고 나면 나머지 bone들은 일직선이 되어 버리기 때문입니다. 즉, 뼈가 2개를 넘어가는 순간부터 끝점 위치는 맞지만 아래 사진처럼 돼서 게임에 사용하기엔 부자연스럽습니다.
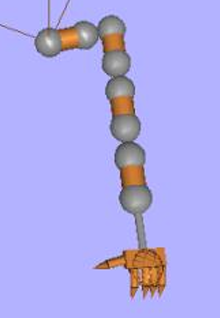
- FABRIK (Forward and Backward Reaching Inverse Kinematics)
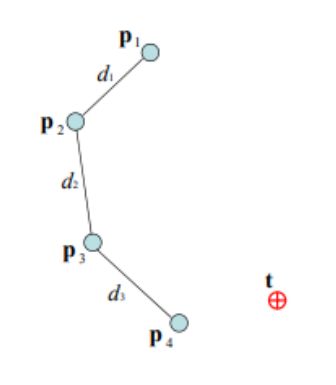
- joint들 사이 거리를 계산해 구한 bone들의 길이의 합과 첫 관절에서 끝점 사이 거리를 비교해서 도달 가능한지 확인합니다.
- 도달 가능하다면 Forward 단계와 Backward 단계로 나눠서 둘을 번갈아가면서 해를 구합니다.
- 끝점 위치가 원하는 위치에 충분히 도달할 때까지 2번 과정을 반복합니다.
Forward 단계
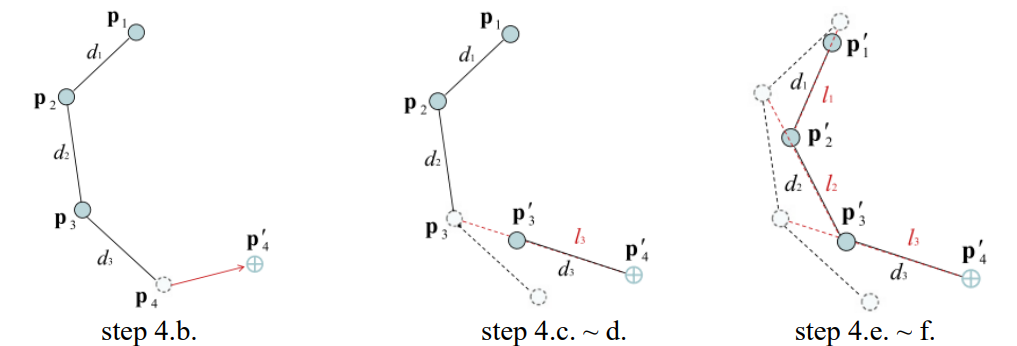
- 끝점(p4)을 원하는 끝점 위치(p’4)로 옮깁니다.
- 끝점 바로 전 관절(p3)에서 끝점을 잇는 직선 상에서 끝점에서 뼈길이(d3)만큼 떨어진 위치로 전 관절(p3)을 옮깁니다.
- 2번 과정을 이전 관절들에 대해 진행해서 체인의 시작 관절 (p1)까지 순차적으로 진행합니다.
Backward 단계
Forward 단계를 진행하면 체인의 시작 관절 위치가 변경됩니다. 이 관절 위치를 다시 맞춰주기 위해 해당 단계를 진행합니다.
Backward 단계는 체인의 시작 관절 → 끝점 순서대로 Forward 단계와 동일한 방식을 진행하는 것입니다.
게임에서의 IK
현실적인 게임을 만들기 위해서는 환경, 상황에 따라 굉장히 많은 캐릭터 움직임(애니메이션)이 발생합니다. 이러한 모든 움직임을 미리 다 정의해두는 것과, 이를 적용하는 것은 사실상 불가능합니다. (또한 애니메이션 제작에는 큰 비용이 듭니다.)
따라서 상황에 맞는 애니메이션을 그때그때 계산하는 기술들이 필요합니다. 그중 하나가 역운동학입니다.
예를 들어 캐릭터가 팔을 뻗고 벽을 향해 계속해서 걸어가는 상황에서, 손이 벽에 닿은 이후부터는 손의 위치가 벽을 뚫고 계속해서 앞으로 가는 것이 아니라 벽에 닿은 위치에 고정되고 이에 따라 팔이 접혀야 자연스러울 것입니다. 이때, 팔이 접히는 회전 각도를 구하기 위해 손 위치(끝점)의 위치를 벽 위치로 두고 역운동학을 통해 이 회전 각도를 구하여 적용할 수 있습니다.
Two-Bone IK
Two-Bone IK가 게임에서 많이 사용됩니다. 그 이유는,
첫 번째는, 제2코사인법칙을 사용하는 Heuristic한 방법으로 복잡한 계산이 필요 없기 때문입니다.
두 번째는, 반복적으로 값을 고쳐 자연스러운 캐릭터 애니메이션을 만드는 IK 방법들은 여러 번의 계산으로 비용이 큽니다. 반복적으로 고칠 필요 없는 Triangulation IK는 뼈가 두 개를 넘어가게 되면 자연스럽지 못합니다. 따라서 적은 비용으로 자연스러운 캐릭터 애니메이션 IK를 구현하기 위해 뼈 두 개에 대해 Triangulation IK를 사용하는 Two-Bone IK를 주로 사용합니다.
세 번째는, 게임에서 사람 캐릭터에 사용하는 경우 (어깨, 팔꿈치), (엉덩이, 무릎), (팔꿈치, 손목), (무릎, 발목) 이렇게 두 관절로 끊기 적합하기 때문입니다.
Two-Bone IK 원리
제2코사인법칙은 삼각형에서 두 변의 길이와 그 사이각을 알 때 나머지 한 변의 길이를 구하는 방법입니다.
$c^2=a^2+b^2−2ab⋅cos(C)$
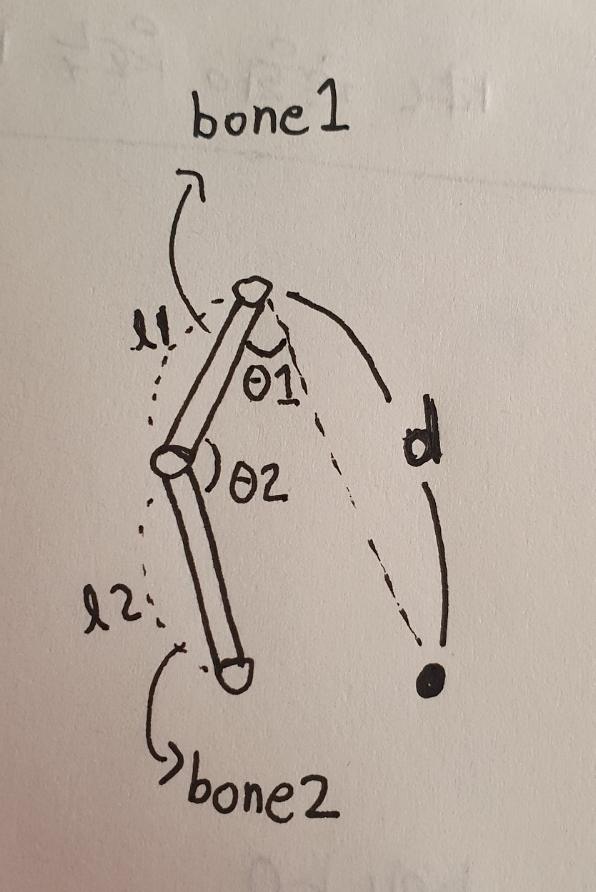
두 bone으로 이루어진 체인의 시작점에 연결된 bone1의 길이 l1과 끝점에 연결된 bone2의 길이 l2와 체인의 시작 관절부터 원하는 끝점 위치 사이의 거리 d를 사용합니다. 제2코사인법칙을 사용해서 회전해야 하는 각도 θ1과 θ2를 구합니다 (아크코사인 활용).
θ1은 위의 제2코사인법칙 식에 a = l1, b = d, c = l2 를 사용해서 구합니다.
θ2는 위의 제2코사인법칙 식에 a = l1, b = l2, c = d 를 사용해서 구합니다.

Leave a comment