[Data Structure] B-tree, B+tree, B*tree

B-tree

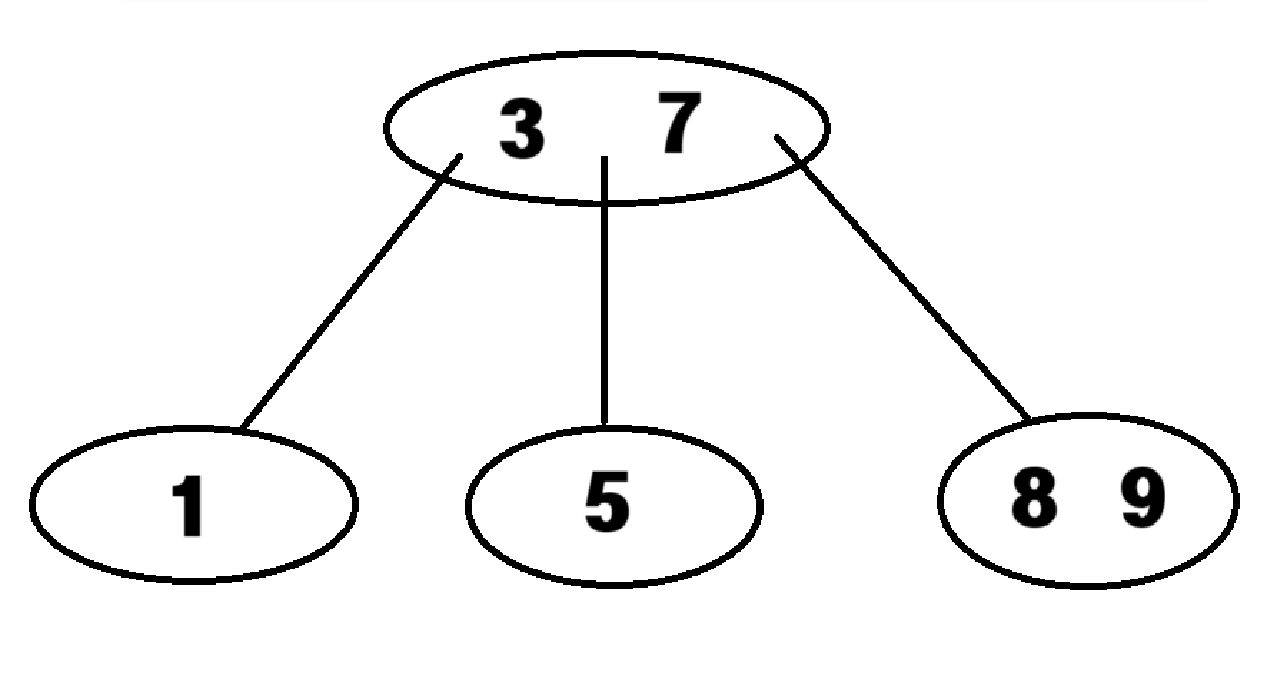
• B-tree는 이진 트리와 다르게 하나의 노드에 여러 개의 데이터(key)를 저장할 수 있으며, 3개 이상의 자식을 가질 수 있다.
• 차수는 각 노드가 가질 수 있는 최대 자식 노드의 수이다. (차수가 3인, 3차 B-tree를 2-3 tree라고 한다.)
• 부모 노드는 최대 [차수 – 1] 개의 key를 가질 수 있다.
• 루트 노드와 리프 노드를 제외한 모든 노드는 최소한 ROUNDUP(차수/2)개의 자식 노드를 가져야 하며, 루트 노드를 제외한 모든 노드는 최소한 ROUNDUP(차수/2) – 1 개의 key를 가져야 한다.
• internal 노드(적어도 하나의 자식을 가지는 노드)의 key 수가 x개면 자녀 노드의 수는 반드시 x+1개여야 한다.
• 값들이 정렬되어 있다.

알고리즘

삽입

• 삽입은 항상 leaf 노드에 한다.
• 노드가 넘치면 가운데 key를 기준으로 좌우 key들을 분할하고 가운데 key는 승진한다.

삭제

• 삭제도 항상 leaf 노드에서 한다. (internal 노드라면 leaf 노드와 데이터 바꾸고 leaf에서 삭제)
• 삭제 후 최소 key 수보다 적어졌다면 재조정한다.

시간 복잡도

• 검색, 삽입, 삭제의 평균, 최악 모두 O(logN)

왜 B-tree?

균형이진트리 또한 검색, 삽입, 삭제의 평균, 최악 모두 O(logN)인데,
(균형이진트리 : 트리 높이를 균형이 맞게 유지해서 안정적인 속도를 보장하는 이진 트리. ex) AVL 트리, Red-black tree 등))

해시 사용하면 O(1)인데,

왜?

균형이진트리와 비교

DB는 secondary storage에 저장된다.
데이터를 조회할 때 secondary storage에 최대한 적게 접근하는 것이 성능 면에서 좋다.
block 단위로 읽고 쓰기 때문에 연관된 데이터를 모아서 저장하면 더 효율적으로 읽고 쓸 수 있다.

B-tree는 자식 노드의 수에 제한이 없는 특징 때문에 트리의 높이가 낮아져서 데이터 탐색에서 secondary storage에 접근하는 횟수가 적다.
하나의 노드에 key를 여러 개 저장할 수 있다는 특징 때문에 연관된 데이터들을 block 단위로 읽어오기 좋다.

엄청나게 많은 데이터를 낮은 높이의 트리로 저장할 수 있어서 모든 데이터에 적은 이동으로 접근할 수 있다.

hash와 비교

검색/삽입/삭제 시간 복잡도가 O(1)이라 더 좋다. 하지만 범위 기반 검색이나 정렬에는 사용할 수 없다.

B+tree

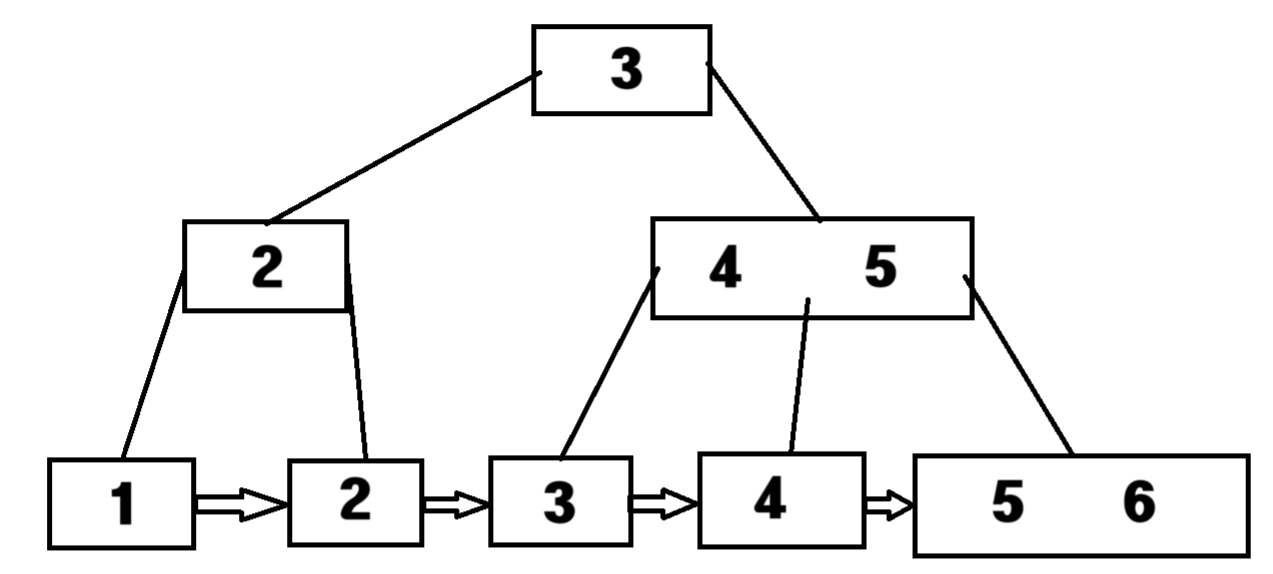
B-tree에서 순차 접근을 하려면 중위 순회(inorder traversal)를 해야한다. 이를 더 좋게 하기 위해 내부 노드들은 오직 키와 포인터만 가지고 인덱스 역할만 하게 하고, 리프 노드만 데이터 값들을 가지게 하고 연결리스트로 연결해놓은 것이 B+tree다. 데이터베이스 수업에서 배우는 다단계 인덱스가 B+tree를 사용한다.

B*tree

B-Tree의 메모리 낭비, 보조 연산 문제를 해결하기 위해 만들어졌다. 쉽게 생각하면 B-tree의 개선 버전이다. 대용량 시스템에서 B-Tree의 운용 시 전체 노드의 상당 부분이 비어있어 메모리 낭비 문제를 초래한다. 그리고 B-Tree의 삽입/삭제 연산 시 노드 혹은 key를 옮기는 등의 작업을 수행하는 분할, 병합 연산을 최소로 줄여 성능을 개선했다.

B-tree는 루트 노드를 제외한 모든 노드는 최소한 ROUNDUP(차수/2) – 1 개의 key를 가져야 했는데, B*tree는 그 수를 늘려서 최소 (차수-1) * 2/3개 이상의 key를 가져야 한다. 즉 최소로 가져야하는 key 값을 늘렸다.
또한 노드가 넘칠 경우 B-tree는 가운데 key를 기준으로 좌우 key들을 분할하고 가운데 key는 승진했는데, B*tree는 노드가 넘치면 일단 형제 노드로 key 값을 재분배하고 만약 모든 형제 노드가 전부 full일 경우에만 B-tree의 분할 연산을 수행한다. 이렇게 분할 연산 빈도를 줄였다.